Fish market
Why only the very best should have offspringStill, some incremental improvements can be made on this algorithm. So far, just the very last element in the population, the scum of the land, was eliminated in each iteration. But, very close to it, where others that didn't deserved the bits they were codified into. Ratcheting up evolutionary pressure might allow us to reach the solution a bit faster.
Besides, anybody who has seen a National Geographic documentary program or two knows that, very often, only the alpha male, after beating anybody else who dares to move in the pack, gets the chance to pass its genetic material to the next generation; some other less violent animals like peacocks have to boast the best of its feathers to be able to attract peahens (if that term exists, anyways). All in all, while many of the worst die, some others lead a very boring life, because they don't get the chance to mate.
These two sad facts of life lead us to the following improvement on the basic evolutionary algorithm:(3rdga.pl; some parts yadda yadda)
#Everything else is the same, except this loop
for ( 1..$generations ) {
for ( my $i = 0; $i < 10; $i ++ ) {
my $chr1 = $population[ rand( $#population/2)];
my $chr2 = $population[ rand( $#population/2)];
#Generate offspring that is better
my $clone1 ={};
my $clone2 ={};
do {
$clone1 = { _str => $chr1->{_str},
_fitness => 0 };
$clone2 = { _str => $chr2->{_str},
_fitness => 0 };
mutate( $clone1 );
mutate( $clone2 );
crossover( $clone1, $clone2 );
$clone1->{_fitness} = fitness( $clone1->{_str} );
$clone2->{_fitness} = fitness( $clone2->{_str} );
} until ( ($clone1->{_fitness} < $population[$#population]->{_fitness}) ||
($clone2->{_fitness} < $population[$#population]->{_fitness}));
if ($clone1->{_fitness} > $population[$#population]->{_fitness}) {
$population[$#population]=$clone1;
} else {
$population[$#population]=$clone1;
}
@population = sort { $a->{_fitness} <=> $b->{_fitness} } @population;
}
|
In this case, first, ten new chromosomes are generated each iteration, one in every iteration of the mutation/crossover loop. This number is completely arbitrary; it corresponds to 10% of the population, which means we are not really introducing a very strong evolutionary pressure. Each time a new chromosome is introduced, population is resorted (and this could probably be done more efficiently by just inserting the new member of the population in the corresponding place and shifting back the rest of the array, but I just didn't want to add a few more lines to the listing). So, each generation, the ten worst are eliminated.
Besides, the elements that will be combined to take part (if they pass) in the next generation, are selected from the elite first half of the (sorted by fitness) population. That introduces an additional element of efficiency: we already know that what is being selected is, at least, above average (above median, actually).
In fact, evolution proceeds faster in this case, but it does not become reflected in the number of iterations taken. Why? Because it decreases the number of iterations needed before offspring "graduates", that is, before they become better than the last element of the population. Thus, on the whole, this algorithm runs a bit faster, but the number of generations needed to reach target is more or less the same.
 | As cattle breeders have known for a long time, breeding using the best material available actually improves performance of evolutionary algorithms. Use it judiciously. |
However, magic numbers such as the "10" and "half population" inserted in that program are not good, even in a Perl program. We can alter that program a bit, making the selective pressure variable, so that we can select the proportion of elements that will be selected for reproduction from the command line, giving the fourth example so far.
With this example we can check what is the effect of reproduction selectivity in the time the algorithm takes to converge to the correct solution. We run it several times, with selectivity ranging from 10% (parents are selected from the best 10% of the population) to 90% (just 10% are considered not suitable for breeding). The effects are plotted in the following figure:

Comparison of the evolutionary algorithm for different reproductive selectivity. In green we can see the original line, in which the reproductive pool was the best half of the population. The most elitist selection strategy seems to be the hands-up winner, with the rest needing increasing number of evaluations to reach target with decreasing selective pressure.
Looks like being selective with the reproductive pool is beneficial, but we should not forget we are solving a very simple problem. If we take that to the limit, choosing just the two best (in each generation) to mutate and recombine, we would be impoverishing the genetic pool, even as we would be exploiting what has been achieved so far. On the other hand, using all the population disregarding fitness for mutation and mating explores the space more widely, but we are reducing the search to a random one.
 | Keeping the balance between exploration and exploitation is one of the most valued skills in evolutionary computation. Too much exploration reduces an evolutionary algorithm to random search, and too much exploitation reduces it to hill-climbing. |
The reduction of the diversity is something any practitioner is usually afraid, and is produced by too much exploitation, or, in another terms, by the overuse of a small percentage of individuals in the population. This leads to inbreeding, and, ultimately, to stagnation of the population in a point from which it cannot escape. These points are usually local minima, and are akin to the problems faced by reduced and segmented wildlife populations: its effects, and increased vulnerability to plagues, has been studied, for instance, in the Ngorongoro's population of lions.
So far, we have used a greedy strategy to select new candidates for inclusion in the population: only when an operation results in something better than the worst in the population, we give it the right to life, and insert in in the new population. However, we already have a mechanism in place for improving the population: use just a part of the population for reproduction, based on its fitness, and substitute always the worst. Even if, in each generation, we do not obtain all individuals better than before, it is enough to find at least a few ones that are better to make the population improve. That is what we do in the 5th example 5thga.pl. The number of individuals generated in each iteration can be passed in the command line, and the reproductive selectivity can be also altered, as before. Results are plotted in the following figure:
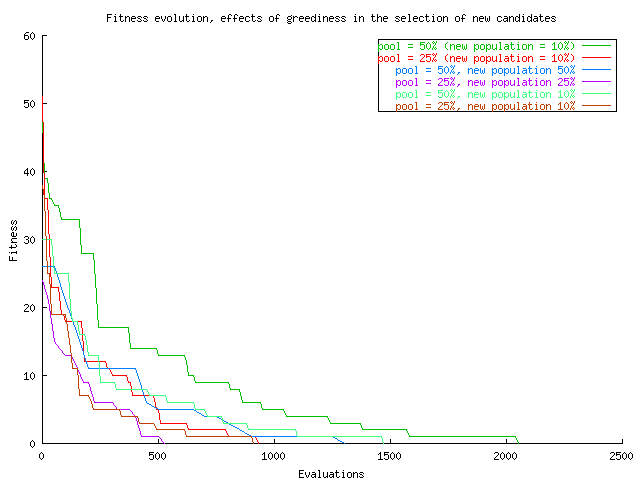
(Bad) Comparison among an evolutionary algorithm in which, in each generation, 25 new elements are generated, chosen from the 25 best (pinkish) or 10 best (brown), 50 and 50 (blue) or 10 (light blue), and the previous results (where 10 new elements were renewed every generation). Not using a greedy algorithm to select new individuals, does not make results much worse, even if we take into account that we are not comparing the same thing here, because the actual number of evaluations until one better than before is reached is not measured; the number of evaluations shown. Other than that, the effect of renewing a different proportion of the population depends on how many we have chosen in advance to substitute the eliminated population: if the genetic pool is big, substituting more improves results (green vs dark and light blue lines, 10% and 50% substitution rate); if the genetic pool is small (25%), results look better if more chromosomes are substituted (pink vs brown and red). This might be due to the balance between exploration and exploitation: by generating too many new elements (50% substitution rate) we are moving the balance towards exploration, turning the algorithm into a random search; but if the pool is small (25%), generating too few would shift the balance toward exploitation, going to the verge of inbreeding; in that case, generating more individuals by crossover leads to better results.
 | As David Goldberg said in Zen and the Art of Genetic Algorithms, let Nature be your guide. There is no examination board in Nature that decides what's fit for being given birth or not; even so, species adapt to their environment along time. Evolutionary algorithms follow this advice. |
 | There are a couple of lessons to be learned from this last example: first, plain selection by comparison of each new individual with the current generation is enough for improving results each step; second, the balance between reproductive and eliminative selectivity is a tricky thing, and has a big influence in results. In some case, being very selective for reproduction and renewing a big part of the population might yield good results, but, in most cases, it will make the algorithm decay to random search and lead to stagnation. |